Make Moon (Sklearn)




1. 1. Les données

Les données
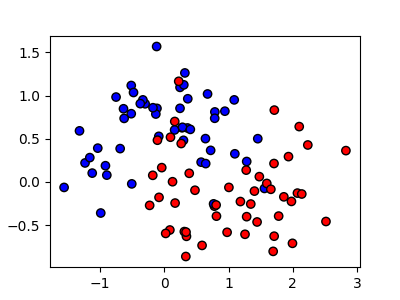
from sklearn.datasets import make_moons

X, y = make_moons(n_samples=100, noise=0.3, random_state=42)
plt.figure(figsize=(4, 3))
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k', cmap='bwr')




2. 2. Apprentissage

L'apprentissage'
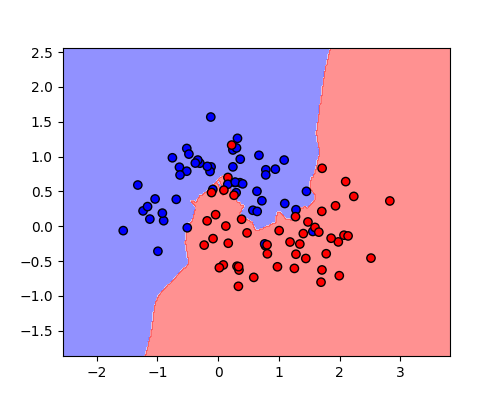
from sklearn.datasets import make_moons
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
from sklearn.neighbors import KNeighborsClassifier

X, y = make_moons(n_samples=100, noise=0.3, random_state=42)
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X, y)

h = .02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.figure(figsize=(5, 4))
plt.contourf(xx, yy, Z, alpha=0.5, cmap='bwr')
plt.scatter(X[:, 0], X[:, 1], c=y, edgecolor='k', cmap='bwr')




3. 3. Matrice de confusion


Confusion Matrix
y_pred = knn.predict(X)
cm = confusion_matrix(y, y_pred)
[[45  5]
 [ 2 48]]
Confusion Matrix display
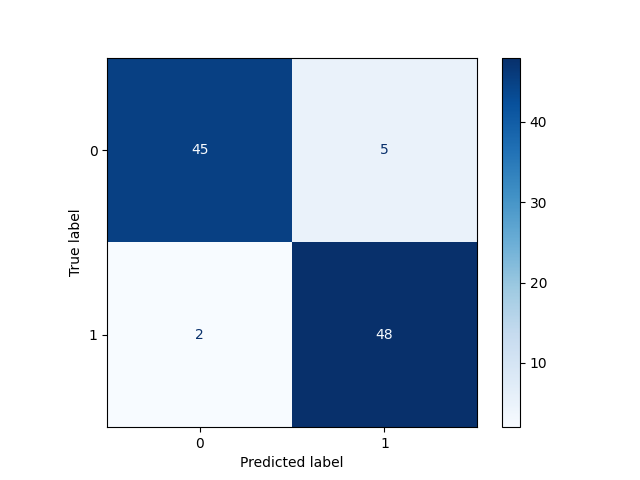
disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=knn.classes_)
disp.plot(cmap=plt.cm.Blues)
plt.title = ('Confusion Matrix for KNN on make_moons Dataset')




5. 5. Accuracy (Exactitude)

Accuracy (Exactitude) = Proportion de bonnes réponses, qu'elles soient Positives ou négatives
= (TP + TN) / (Positives + Negatives)
/!\ Cette métrique ne prend pas en compte les faux positifs et faux négatifs, ce qui donne de mauvains résultats en cas de classification déséquilibrée.
/!\ Exemple : 100 individus, 2 malades, 98 en bonne santé. Le modèle prédit 0 malades, 100 en bonne santé.
/!\ Accuracy = (TP + TN) / 100 = (98 + 0) / 100 = 98%

Matrice de confusion

[[45  5]
 [ 2 48]]
TN (True Negative) = 45
FP (False Positive) = 5
FN (False Negative) = 2
TP (True Positive) = 48
Accuracy score = (TP + TN)/(TN + TP + FN + FP) = 0.93
93% de bonnes estimations par le modèle

Acuracy score
from sklearn.metrics import acuracy_score
acuracy = acuracy_score(y, y_pred)
0.93
Accuracy score = 93%



6. 6. Precision

Precision = Proportion de toutes les prédictions positives qui sont justes
= PPV (Positive predictive value) = Nombre de vrais positifs / Nombre de prédictions classées comme positives
= TP / (TP + FP)

Matrice de confusion

[[45  5]
 [ 2 48]]
TN (True Negative) = 45
FP (False Positive) = 5
FN (False Negative) = 2
TP (True Positive) = 48
precision = TP/(TP + FP) = 0.9056603773584906
91% des prédictions positives sont justes

FDR (False Discovery Rate) = 1 - Precision = 9%

Précision
from sklearn.metrics import precision_score
precision = precision_score(y, y_pred)
0.9056603773584906
Précision = 91%
Precision = 0 => Toutes les prédictions positives sont fausses
Précision = 0.5 => La moitié des prédictions positives sont fausses
Precision = 1 => Toutes les prédictions positives sont bonnes
Utiliser la précision lorque ce qui compte le plus est la capacité du modèle à ne pas se tromper dans ses prédictions positives
Ne pas prédire qu'un patient est malade alors qu'il ne l'est pas
Par exemple : Ne pas prédire qu'un patient est malade alors qu'il ne l'est pas



7. 7. Recall (Rappel)

Recall (Sensitivity) = Proportion de valeurs positives qui ont identifiées par le modèle (correctement ou pas)
(Sensitivity, probability of detection, hit rate, power)
= TPR (True Positive Rate) = Nombre de vrais positifs / Nombre total de valeurs positives
= TP / (TP + FN)

Matrice de confusion

[[45  5]
 [ 2 48]]
TN (True Negative) = 45
FP (False Positive) = 5
FN (False Negative) = 2
TP (True Positive) = 48
recall = TP/(TP + FN) = 0.96
96% des des valeurs positivies ont été trouvées

FNR (False Negative Rate, miss rate) = 1 - Recall = 4%

Recall
from sklearn.metrics import recall_score
recall = recall_score(y, y_pred)
0.96
Recall = 96%
Recall = 0 => Aucun positif n'a été trouvé
Recall = 0.5 => La moitié des positifs a été trouvé
Precision = 1 => Tous les positifs ont été trouvés
Utiliser le recall lorque ce qui compte le plus est la capacité du modèle à trouver un maximum de positifs, quitte à faire quelques erreurs
Par exemple: identifier tous les malades, même si au passage on confond quelques personnes pour des non-malades



8. 8. Courbe de Précision / Recall

Objectif : Avoir le meilleur compromis (trade-off) entre Précision et Recall
(Aucune des prédictions positives ne sont correctes) 0 < Précision < 1 (Toutes les prédictions positives sont correctes)
(Aucun positif n'a été trouvé) 0 < Recall < 1 (Tous les poditifs ont été trouvés)
Indicateur : 0 < Area under curve <1
from sklearn.metrics import precision_recall_curve
knn.predict_proba(X)
[[0.         1.        ]
 [0.66666667 0.33333333]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [1.         0.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [0.         1.        ]
 [1.         0.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [0.66666667 0.33333333]
 [1.         0.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [1.         0.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [1.         0.        ]
 [1.         0.        ]
 [1.         0.        ]
 [1.         0.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [1.         0.        ]
 [1.         0.        ]
 [0.66666667 0.33333333]
 [1.         0.        ]
 [1.         0.        ]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [0.66666667 0.33333333]
 [0.         1.        ]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [0.33333333 0.66666667]
 [0.33333333 0.66666667]
 [0.66666667 0.33333333]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.         1.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [0.         1.        ]
 [0.66666667 0.33333333]
 [0.33333333 0.66666667]
 [1.         0.        ]
 [0.33333333 0.66666667]
 [0.33333333 0.66666667]
 [0.33333333 0.66666667]
 [0.33333333 0.66666667]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.         1.        ]
 [1.         0.        ]
 [0.         1.        ]
 [0.33333333 0.66666667]]
Precision-Recall Curve
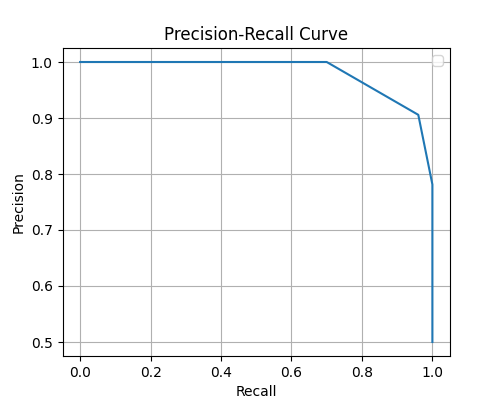
precision, recall, thresholds = precision_recall_curve(y, knn.predict_proba(X)[:,1])

plt.figure(figsize=(5, 4))
plt.plot(recall, precision)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision-Recall Curve')
plt.legend(loc='best')
plt.grid()




9. 9. Score f1

F1 Score = (2 x Precision x Recall) / (Precision + Recall)
C'est la moyenne harmonique entre la Précision et le Recall
Moyenne harmonique
Moyenne trajet aller-retour avec 40km/h aller et 60km/h retour
Moyenne arithmétique -> Mais pas la même durée pour chaque trajet.
Moyenne harmonique -> sur l'ensemble du temps
Intérêt pour le Score F1 : Si l'une des deux mesure (P) ou (R) est faible, la moyenne harmonique reflète mieux la faiblesse globale.

f1 Score
precision = precision_score(y, y_pred)
recall = recall_score(y, y_pred)
f1 = (2 * precision * recall) / (precision + recall)
0.9320388349514563

f1 Score (sklearn)
from sklearn.metrics import f1_score
f1 = f1_score(y, y_pred)
0.9320388349514563



10. 10. Classification Report


Classification Report (sklearn)
from sklearn.metrics import classification_report
classification = classification_report(y, y_pred)
              precision    recall  f1-score   support

           0       0.96      0.90      0.93        50
           1       0.91      0.96      0.93        50

    accuracy                           0.93       100
   macro avg       0.93      0.93      0.93       100
weighted avg       0.93      0.93      0.93       100



11. 11. ROC Curve et le score AUC

Le ROC (Receiver Operating Characteristic) est une courbe permettant de régler les modèles de classification bibnaire afin de trouver le bon compromis entre
True Positive Rate (TPR) - Proportion de valeurs positives qui ont été identifiées par le modèle (Recall)
False Positive Rate (FPR) - Proportion de valeurs négatives qui ont été incorrectement identifiées comme positives par le modèle (Erreur de type 1)

ROC
from sklearn.metrics import roc_curve, RocCurveDisplay, roc_auc_score
y_score = knn.predict_proba(X)
roc = roc_curve(y, y_score=y_score[:, 1])
(array([0.  , 0.  , 0.1 , 0.28, 1.  ]), array([0.  , 0.7 , 0.96, 1.  , 1.  ]), array([       inf, 1.        , 0.66666667, 0.33333333, 0.        ]))
fpr, tpr, thresholds = roc_curve(y, y_score=y_score[:, 1])
FPR (False Positive Rate)
[0.   0.   0.1  0.28 1.  ]
TPR (True Positive Rate)
[0.   0.7  0.96 1.   1.  ]
Thresholds
[       inf 1.         0.66666667 0.33333333 0.        ]
ROC Curve
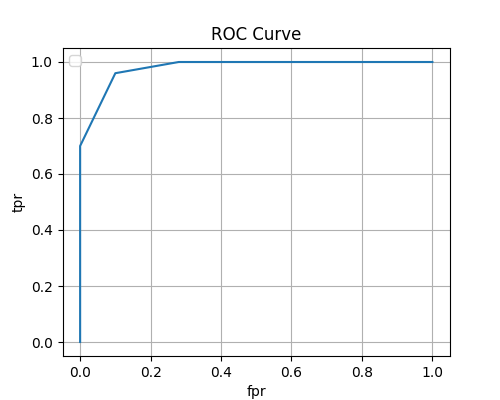
fpr, tpr, thresholds = roc_curve(y, y_score=y_score[:, 1])

plt.figure(figsize=(5, 4))
plt.plot(fpr, tpr)
plt.xlabel('fpr')
plt.ylabel('tpr')
plt.title('ROC Curve')
plt.legend(loc='best')
plt.grid()


ROC AUC Score
auc = roc_auc_score(y, y_score=y_score[:,1])
0.9794
ROC Curve (sklearn)
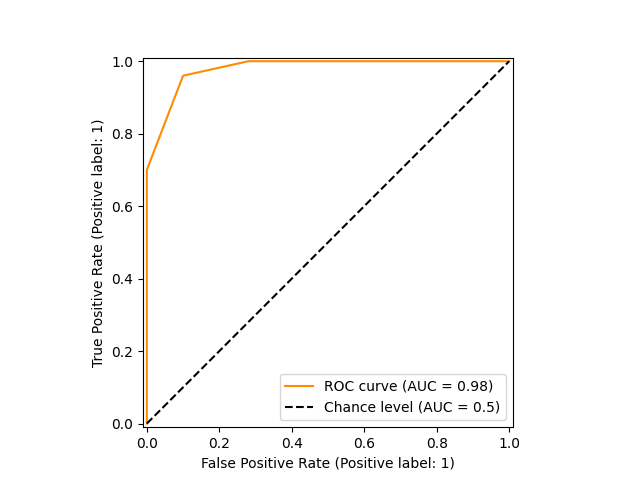
fpr, tpr, thresholds = roc_curve(y, y_score=y_score[:, 1])

display = RocCurveDisplay.from_predictions(
   y,
   y_score[:, 1],
   color = 'darkorange',
   plot_chance_level=True,
)
display.ax_.set(
   xlabel='False Positive Rate',
   ylabel='True Positive Rate',
   title='ROC curve'
)
display.plot()