Diamonds - Preprocessing




1. 1. Analyse du dataset


Analyse du dataset
df = sns.load_dataset('diamonds')
df.head()
   carat      cut color clarity  depth  table  price     x     y     z
0   0.23    Ideal     E     SI2   61.5   55.0    326  3.95  3.98  2.43
1   0.21  Premium     E     SI1   59.8   61.0    326  3.89  3.84  2.31
2   0.23     Good     E     VS1   56.9   65.0    327  4.05  4.07  2.31
3   0.29  Premium     I     VS2   62.4   58.0    334  4.20  4.23  2.63
4   0.31     Good     J     SI2   63.3   58.0    335  4.34  4.35  2.75
df.describe()
              carat         depth  ...             y             z
count  53940.000000  53940.000000  ...  53940.000000  53940.000000
mean       0.797940     61.749405  ...      5.734526      3.538734
std        0.474011      1.432621  ...      1.142135      0.705699
min        0.200000     43.000000  ...      0.000000      0.000000
25%        0.400000     61.000000  ...      4.720000      2.910000
50%        0.700000     61.800000  ...      5.710000      3.530000
75%        1.040000     62.500000  ...      6.540000      4.040000
max        5.010000     79.000000  ...     58.900000     31.800000

[8 rows x 7 columns]

Avec suppression des valeurs nulles
df.query('x > 0 and y > 0 and z > 0')
df.describe()
              carat         depth  ...             y             z
count  53920.000000  53920.000000  ...  53920.000000  53920.000000
mean       0.797698     61.749514  ...      5.734887      3.540046
std        0.473795      1.432331  ...      1.140126      0.702530
min        0.200000     43.000000  ...      3.680000      1.070000
25%        0.400000     61.000000  ...      4.720000      2.910000
50%        0.700000     61.800000  ...      5.710000      3.530000
75%        1.040000     62.500000  ...      6.540000      4.040000
max        5.010000     79.000000  ...     58.900000     31.800000

[8 rows x 7 columns]



2. 1. Créez une variable volume


Nouvelle colonne volume = x * y * z
df['volume'] = df['x'] * df['y'] * df['z']
df.head()
   carat      cut color clarity  depth  ...  price     x     y     z     volume
0   0.23    Ideal     E     SI2   61.5  ...    326  3.95  3.98  2.43  38.202030
1   0.21  Premium     E     SI1   59.8  ...    326  3.89  3.84  2.31  34.505856
2   0.23     Good     E     VS1   56.9  ...    327  4.05  4.07  2.31  38.076885
3   0.29  Premium     I     VS2   62.4  ...    334  4.20  4.23  2.63  46.724580
4   0.31     Good     J     SI2   63.3  ...    335  4.34  4.35  2.75  51.917250

[5 rows x 11 columns]



3. 2. Créez une variable qui donne le rapport carat / volume (densité apparente)


Nouvelle Colonne density = carat / volume
df['volumne'] = df['x'] * df['y'] * df['z']
df['density'] = df['carat'] / df['volume']
df.head()
   carat      cut color clarity  depth  ...     x     y     z     volume   density
0   0.23    Ideal     E     SI2   61.5  ...  3.95  3.98  2.43  38.202030  0.006021
1   0.21  Premium     E     SI1   59.8  ...  3.89  3.84  2.31  34.505856  0.006086
2   0.23     Good     E     VS1   56.9  ...  4.05  4.07  2.31  38.076885  0.006040
3   0.29  Premium     I     VS2   62.4  ...  4.20  4.23  2.63  46.724580  0.006207
4   0.31     Good     J     SI2   63.3  ...  4.34  4.35  2.75  51.917250  0.005971

[5 rows x 12 columns]



4. 3. Determinez la corrélation entre ces nouvelles variables et le prix. Ces nouvelles associations sont-elles intéressantes ?

Volume <-> Prix Hypothèse 0
Teste s'il existe une corrélation entre 2 variables continues
H0: Le prix d'un diamand n'est pas correlé au volume du diamand
alpha = 0.02
Enquête de terrain
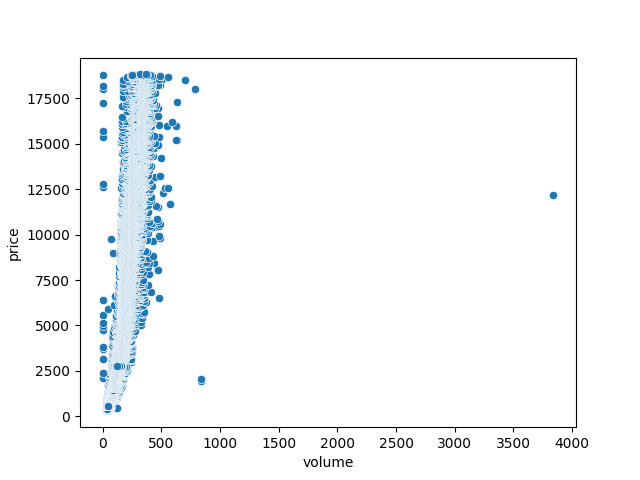
sns.scatterplot(data=df, x='volume', y='price')

Enquête de terrain
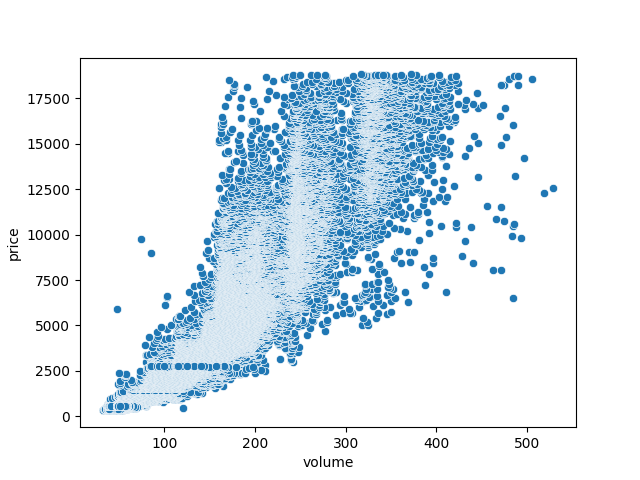
sns.scatterplot(data=df.query("volume <= 550 and volume > 0"), x='volume', y='price')


Test Pearson
pearsonr(df['volume'], df['price'])
PearsonRResult(statistic=np.float64(0.9042546534714132), pvalue=np.float64(0.0))

Conclusion
alpha = 0.02
p_value = pearsonr(df['volume'], df['price']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 0.0
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0
Densité <-> Prix Hypothèse 0
Teste s'il existe une corrélation entre 2 variables continues
H0: Le prix d'un diamand n'est pas correlé à la densité apperente du diamand
alpha = 0.02
Enquête de terrain
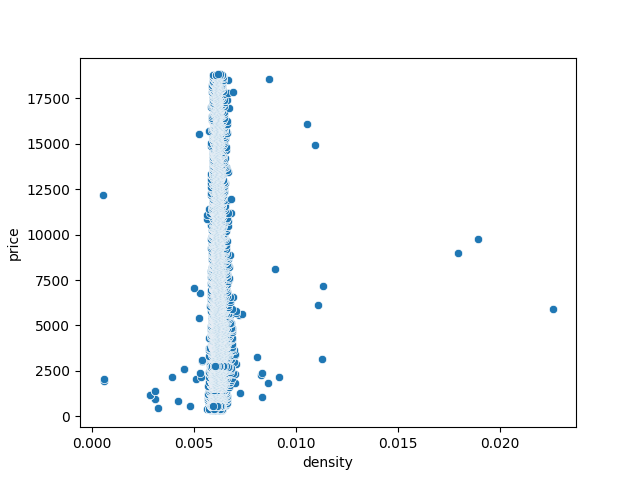
sns.scatterplot(data=df, x='density', y='price')

Enquête de terrain
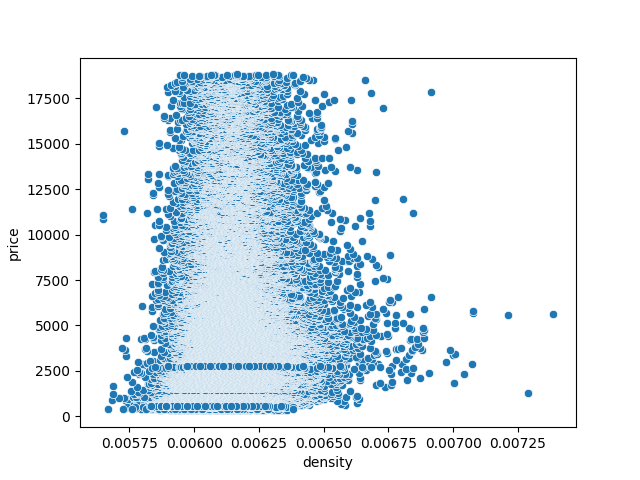
sns.scatterplot(data=df, x='density', y='price')


Test Pearson
pearsonr(df['density'], df['price'])
PearsonRResult(statistic=np.float64(0.14344044273518405), pvalue=np.float64(9.317098024225777e-246))

Conclusion
alpha = 0.02
p_value = pearsonr(df['density'], df['price']).pvalue
if p_value < alpha:
    print('Nous avons suffisament d’évidences pour rejeter H0')
else:
    print('Nous n’avons pas suffisament d’évidences pour rejeter H0')

p_value = 9.317098024225777e-246
p_value < alpha
    Nous avons suffisament d’évidences pour rejeter H0



5. 4. La variable Depth est elle-meme construite sur la base des variables x, y, et z. Saurez-vous trouver laquelle ?




6. 5. Avez-vous d'autres idées de Feature Engineering?




7. Utilisez polynomial features pour tester des combinaisons de degré 2 et dites s'il existe des variables intéressantes.