California Housing
1. 1. Linear Regression
2. 2. Différences
3. 3. MAE (Mean Absolute Error)
4. 4. MSE (Mean Squared Error)
5. 5. RMSE (Root Mean Square Error)
2. 2. Différences
3. 3. MAE (Mean Absolute Error)
4. 4. MSE (Mean Squared Error)
5. 5. RMSE (Root Mean Square Error)
1. 1. Linear Regression
Prédictions
X, y = fetch_california_housing(return_X_y=True)
model = LinearRegression()
model.fit(X, y)
predictions = model.predict(X)
[4.13164983 3.97660644 3.67657094 ... 0.17125141 0.31910524 0.51580363]
Valeurs attendues (en 100 000 $)
y
[4.526 3.585 3.521 ... 0.923 0.847 0.894]
2. 2. Différences
Différences
differences = predictions - y
[-0.39435017 0.39160644 0.15557094 ... -0.75174859 -0.52789476 -0.37819637]
Histogramme des différences
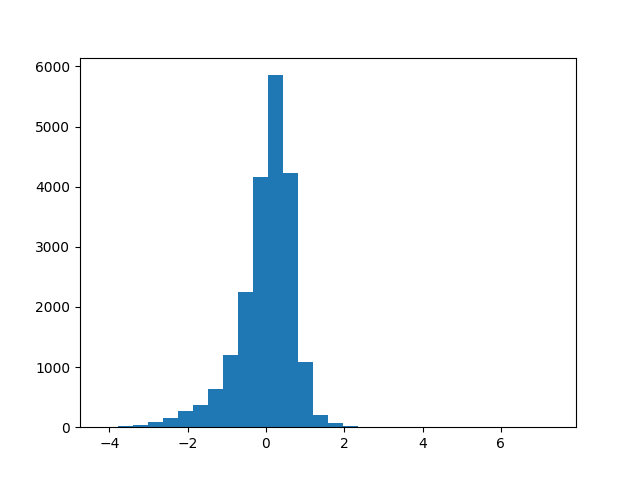
import matplotlib.pyplot as plt
plt.hist(differences, bins=30)

MAE (Mean Absolute Error) = Moyenne des valeurs absolues des différences
result = np.mean(np.abs(differences))
0.5311643817546456
Boxplot des différences
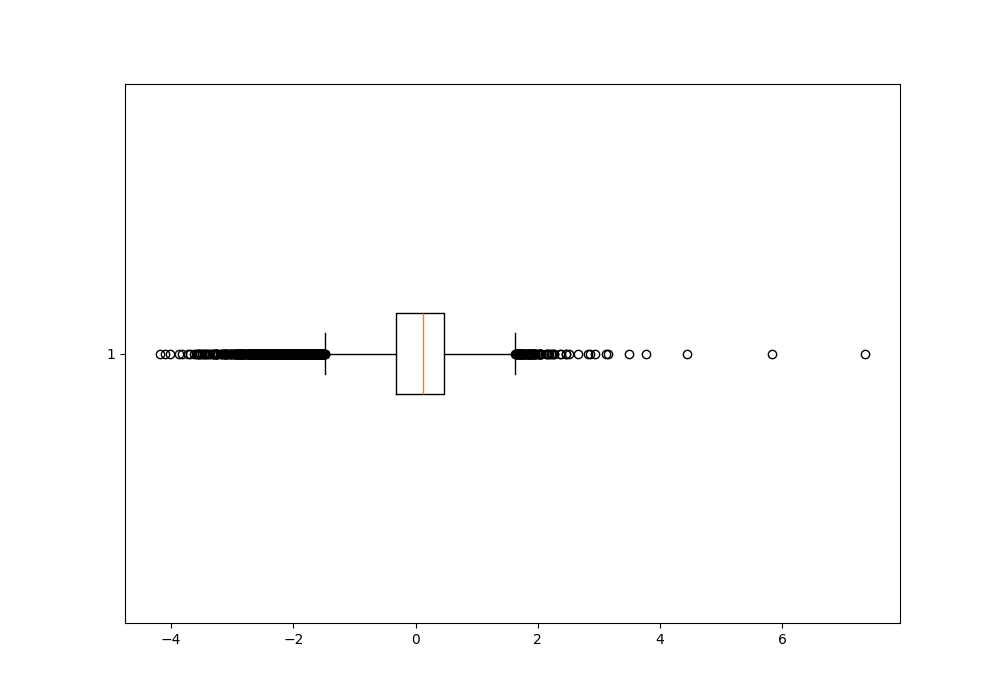
fig = plt.figure(figsize =(10, 4))
plt.boxplot(differences, vert=False)

3. 3. MAE (Mean Absolute Error)
MAE
from sklearn.metrics import mean_absolute_error
result = mean_absolute_error(y_true=y, y_pred=predictions)
0.5311643817546456
4. 4. MSE (Mean Squared Error)
MSE
from sklearn.metrics import mean_squared_error
result = mean_squared_error(y_true=y, y_pred=predictions)
0.5243209861846072
5. 5. RMSE (Root Mean Square Error)
RMSE
from sklearn.metrics import root_mean_squared_error
result = root_mean_squared_error(y_true=y, y_pred=predictions)
0.7241001216576387